[转]10种机器学习算法Part.1
阅读英文原文,请访问如下链接
http://www.analyticsvidhya.com/blog/2015/08/common-machine-learning-algorithms/
广义来说,有三种机器学习算法
1、 监督式学习
Supervised
工作机制:这个算法由一个目标变量或结果变量(或因变量)组成。这些变量由已知的一系列预示变量(自变量)预测而来。利用这一系列变量,我们生成一个将输入值映射到期望输出值的函数。这个训练过程会一直持续,直到模型在训练数据上获得期望的精确度。监督式学习的例子有:回归、决策树、随机森林、K – 近邻算法、逻辑回归等。
2、非监督式学习
Unsupervised
工作机制:在这个算法中,没有任何目标变量或结果变量要预测或估计。这个算法用在不同的组内聚类分析。这种分析方式被广泛地用来细分客户,根据干预的方式分为不同的用户组。非监督式学习的例子有:关联算法和 K – 均值算法。
3、强化学习
Reinforcement
工作机制:这个算法训练机器进行决策。它是这样工作的:机器被放在一个能让它通过反复试错来训练自己的环境中。机器从过去的经验中进行学习,并且尝试利用了解最透彻的知识作出精确的商业判断。 强化学习的例子有马尔可夫决策过程。
常见机器学习算法名单
这里是一个常用的机器学习算法名单。这些算法几乎可以用在所有的数据问题上:
线性回归
逻辑回归
决策树
SVM
朴素贝叶斯
K最近邻算法
K均值算法
随机森林算法
降维算法
Gradient Boost 和 Adaboost 算法
1、线性回归 Linear Regression
线性回归通常用于根据连续变量估计实际数值(房价、呼叫次数、总销售额等)。我们通过拟合最佳直线来建立自变量和因变量的关系。这条最佳直线叫做回归线,并且用 Y= a *X + b 这条线性等式来表示。
理解线性回归的最好办法是回顾一下童年。假设在不问对方体重的情况下,让一个五年级的孩子按体重从轻到重的顺序对班上的同学排序,你觉得这个孩子会怎么做?他(她)很可能会目测人们的身高和体型,综合这些可见的参数来排列他们。这是现实生活中使用线性回归的例子。实际上,这个孩子发现了身高和体型与体重有一定的关系,这个关系看起来很像上面的等式。
在这个等式中:
Y:因变量
a:斜率
x:自变量
b :截距
系数 a 和 b 可以通过最小二乘法获得。
参见下例。我们找出最佳拟合直线 y=0.2811x+13.9。已知人的身高,我们可以通过这条等式求出体重。
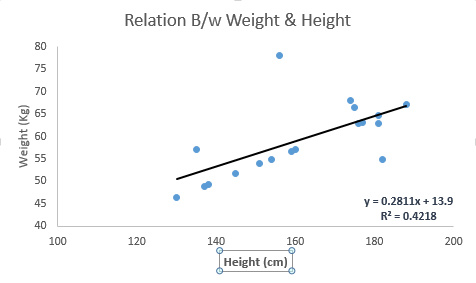
线性回归的两种主要类型是一元线性回归和多元线性回归。一元线性回归的特点是只有一个自变量。多元线性回归的特点正如其名,存在多个自变量。找最佳拟合直线的时候,你可以拟合到多项或者曲线回归。这些就被叫做多项或曲线回归。
Python Code
#Import Library
#Import other necessary libraries like pandas, numpy...
from sklearn import linear_model
#Load Train and Test datasets
#Identify feature and response variable(s) and values must be numeric and numpy arrays
x_train=input_variables_values_training_datasets
y_train=target_variables_values_training_datasets
x_test=input_variables_values_test_datasets
# Create linear regression object
linear = linear_model.LinearRegression()
# Train the model using the training sets and check score
linear.fit(x_train, y_train)
linear.score(x_train, y_train)
#Equation coefficient and Intercept
print('Coefficient:', linear.coef_)
print('Intercept:', linear.intercept_)
#Predict Output
predicted= linear.predict(x_test)R Code
#Load Train and Test datasets #Identify feature and response variable(s) and values must be numeric and numpy arrays x_train <- input_variables_values_training_datasets y_train <- target_variables_values_training_datasets x_test <- input_variables_values_test_datasets x <- cbind(x_train,y_train)# Train the model using the training sets and check scorelinear <- lm(y_train ~ ., data = x) summary(linear)#Predict Output predicted= predict(linear,x_test)
2、逻辑回归 Logistic Regression
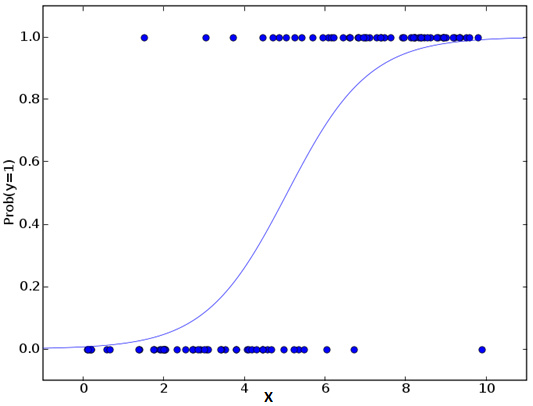
别被它的名字迷惑了!这是一个分类算法而不是一个回归算法。该算法可根据已知的一系列因变量估计离散数值(比方说二进制数值 0 或 1 ,是或否,真或假)。简单来说,它通过将数据拟合进一个逻辑函数来预估一个事件出现的概率。因此,它也被叫做逻辑回归。因为它预估的是概率,所以它的输出值大小在 0 和 1 之间(正如所预计的一样)。
让我们再次通过一个简单的例子来理解这个算法。
假设你的朋友让你解开一个谜题。这只会有两个结果:你解开了或是你没有解开。想象你要解答很多道题来找出你所擅长的主题。这个研究的结果就会像是这样:假设题目是一道十年级的三角函数题,你有 70%的可能会解开这道题。然而,若题目是个五年级的历史题,你只有30%的可能性回答正确。这就是逻辑回归能提供给你的信息。
从数学上看,在结果中,几率的对数使用的是预测变量的线性组合模型。
odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
ln(odds) = ln(p/(1-p))
logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
在上面的式子里,p 是我们感兴趣的特征出现的概率。它选用使观察样本值的可能性最大化的值作为参数,而不是通过计算误差平方和的最小值(就如一般的回归分析用到的一样)。
现在你也许要问了,为什么我们要求出对数呢?简而言之,这种方法是复制一个阶梯函数的最佳方法之一。我本可以更详细地讲述,但那就违背本篇指南的主旨了。
Python Code
#Import Library
from sklearn.linear_model
import LogisticRegression
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create logistic regression object
model = LogisticRegression()
# Train the model using the training sets and check score
model.fit(X, y)
model.score(X, y)
#Equation coefficient and Interceptprint('Coefficient:
', model.coef_)
print('Intercept:
', model.intercept_)
#Predict Output
predicted= model.predict(x_test)R Code
x <- cbind(x_train,y_train)# Train the model using the training sets and check scorelogistic <- glm(y_train ~ ., data = x,family='binomial') summary(logistic)#Predict Output predicted= predict(logistic,x_test)
更进一步:
你可以尝试更多的方法来改进这个模型:
加入交互项
精简模型特性
使用正则化方法
使用非线性模型
3、决策树 Decision Tree
这是我最喜爱也是最频繁使用的算法之一。这个监督式学习算法通常被用于分类问题。令人惊奇的是,它同时适用于分类变量和连续因变量。在这个算法中,我们将总体分成两个或更多的同类群。这是根据最重要的属性或者自变量来分成尽可能不同的组别。想要知道更多,可以阅读:简化决策树。
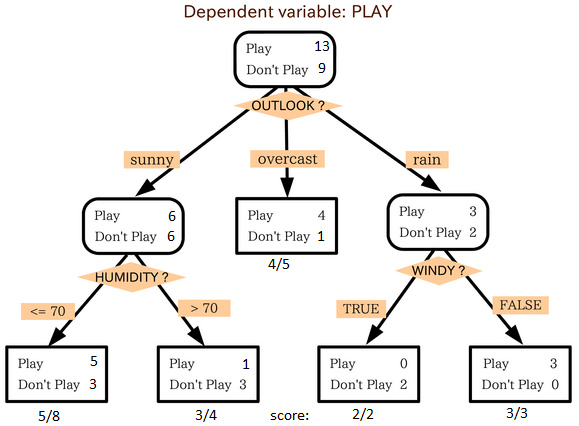
来源: statsexchange
在上图中你可以看到,根据多种属性,人群被分成了不同的四个小组,来判断 “他们会不会去玩”。为了把总体分成不同组别,需要用到许多技术,比如说 Gini、Information Gain、Chi-square、entropy。
理解决策树工作机制的最好方式是玩Jezzball,一个微软的经典游戏(见下图)。这个游戏的最终目的,是在一个可以移动墙壁的房间里,通过造墙来分割出没有小球的、尽量大的空间。
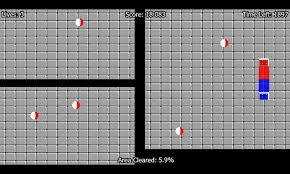
因此,每一次你用墙壁来分隔房间时,都是在尝试着在同一间房里创建两个不同的总体。相似地,决策树也在把总体尽量分割到不同的组里去。
更多信息请见:决策树算法的简化
Python Code
#Import Library #Import other necessary libraries like pandas, numpy... from sklearn import tree #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset# Create tree object model = tree.DecisionTreeClassifier(criterion='gini') # for classification, here you can change the algorithm as gini or entropy (information gain) by default it is gini # model = tree.DecisionTreeRegressor() for regression # Train the model using the training sets and check score model.fit(X, y) model.score(X, y) #Predict Output predicted= model.predict(x_test)
R Code
library(rpart) x <- cbind(x_train,y_train)# grow tree fit <- rpart(y_train ~ ., data = x,method="class")summary(fit)#Predict Output predicted= predict(fit,x_test)
4、支持向量机 SVM
这是一种分类方法。在这个算法中,我们将每个数据在N维空间中用点标出(N是你所有的特征总数),每个特征的值是一个坐标的值。
举个例子,如果我们只有身高和头发长度两个特征,我们会在二维空间中标出这两个变量,每个点有两个坐标(这些坐标叫做支持向量)。
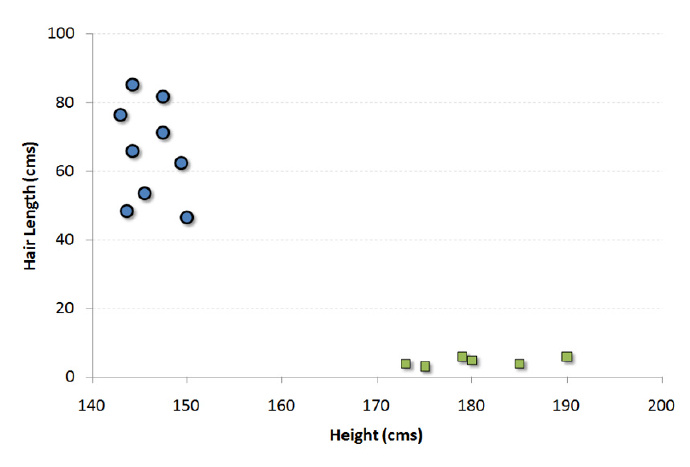
现在,我们会找到将两组不同数据分开的一条直线。两个分组中距离最近的两个点到这条线的距离同时最优化。
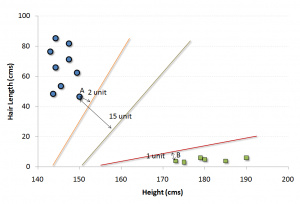
上面示例中的黑线将数据分类优化成两个小组,两组中距离最近的点(图中A、B点)到达黑线的距离满足最优条件。这条直线就是我们的分割线。接下来,测试数据落到直线的哪一边,我们就将它分到哪一类去。
更多请见:支持向量机的简化
将这个算法想作是在一个 N 维空间玩 JezzBall。需要对游戏做一些小变动:
比起之前只能在水平方向或者竖直方向画直线,现在你可以在任意角度画线或平面。
游戏的目的变成把不同颜色的球分割在不同的空间里。
球的位置不会改变。
Python Code
#Import Library from sklearn import svm #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset # Create SVM classification object model = svm.svc() # there is various option associated with it, this is simple for classification. You can refer link, for more detail. # Train the model using the training sets and check score model.fit(X, y) model.score(X, y) #Predict Output predicted= model.predict(x_test)
R Code
library(e1071) x <- cbind(x_train,y_train)# Fitting model fit <-svm(y_train ~ ., data = x)summary(fit)#Predict Output predicted= predict(fit,x_test)
5、朴素贝叶斯 Naive Bayes
在预示变量间相互独立的前提下,根据贝叶斯定理可以得到朴素贝叶斯这个分类方法。用更简单的话来说,一个朴素贝叶斯分类器假设一个分类的特性与该分类的其它特性不相关。举个例子,如果一个水果又圆又红,并且直径大约是 3 英寸,那么这个水果可能会是苹果。即便这些特性互相依赖,或者依赖于别的特性的存在,朴素贝叶斯分类器还是会假设这些特性分别独立地暗示这个水果是个苹果。
朴素贝叶斯模型易于建造,且对于大型数据集非常有用。虽然简单,但是朴素贝叶斯的表现却超越了非常复杂的分类方法。
贝叶斯定理提供了一种从P(c)、P(x)和P(x|c) 计算后验概率 P(c|x) 的方法。请看以下等式:
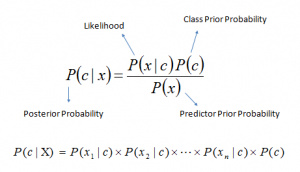
在这里,
P(c|x) 是已知预示变量(属性)的前提下,类(目标)的后验概率
P(c) 是类的先验概率
P(x|c) 是可能性,即已知类的前提下,预示变量的概率
P(x) 是预示变量的先验概率
例子:让我们用一个例子来理解这个概念。在下面,我有一个天气的训练集和对应的目标变量“Play”。现在,我们需要根据天气情况,将会“玩”和“不玩”的参与者进行分类。让我们执行以下步骤。
步骤1:把数据集转换成频率表。
步骤2:利用类似“当Overcast可能性为0.29时,玩耍的可能性为0.64”这样的概率,创造 Likelihood 表格。
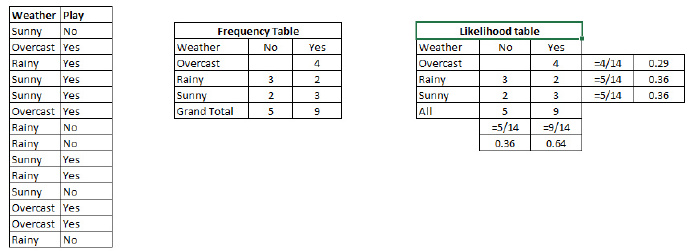
步骤3:现在,使用朴素贝叶斯等式来计算每一类的后验概率。后验概率最大的类就是预测的结果。
问题:如果天气晴朗,参与者就能玩耍。这个陈述正确吗?
我们可以使用讨论过的方法解决这个问题。于是 P(会玩 | 晴朗)= P(晴朗 | 会玩)* P(会玩)/ P (晴朗)
我们有 P (晴朗 |会玩)= 3/9 = 0.33,P(晴朗) = 5/14 = 0.36, P(会玩)= 9/14 = 0.64
现在,P(会玩 | 晴朗)= 0.33 * 0.64 / 0.36 = 0.60,有更大的概率。
朴素贝叶斯使用了一个相似的方法,通过不同属性来预测不同类别的概率。这个算法通常被用于文本分类,以及涉及到多个类的问题。
Python Code
#Import Library from sklearn.naive_bayes import GaussianNB #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset # Create SVM classification object model = GaussianNB() # there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link # Train the model using the training sets and check score model.fit(X, y) #Predict Output predicted= model.predict(x_test)
R Code
library(e1071) x <- cbind(x_train,y_train)# Fitting model fit <-naiveBayes(y_train ~ ., data = x)summary(fit)#Predict Output predicted= predict(fit,x_test)